Binary Math
How are computers performing additions and subtractions.
Binary additions ➕
In binary, there are only two symbols (0, 1). We call binary a base-2 numeral system.
So if we have more than 1 of something, another bit is needed:
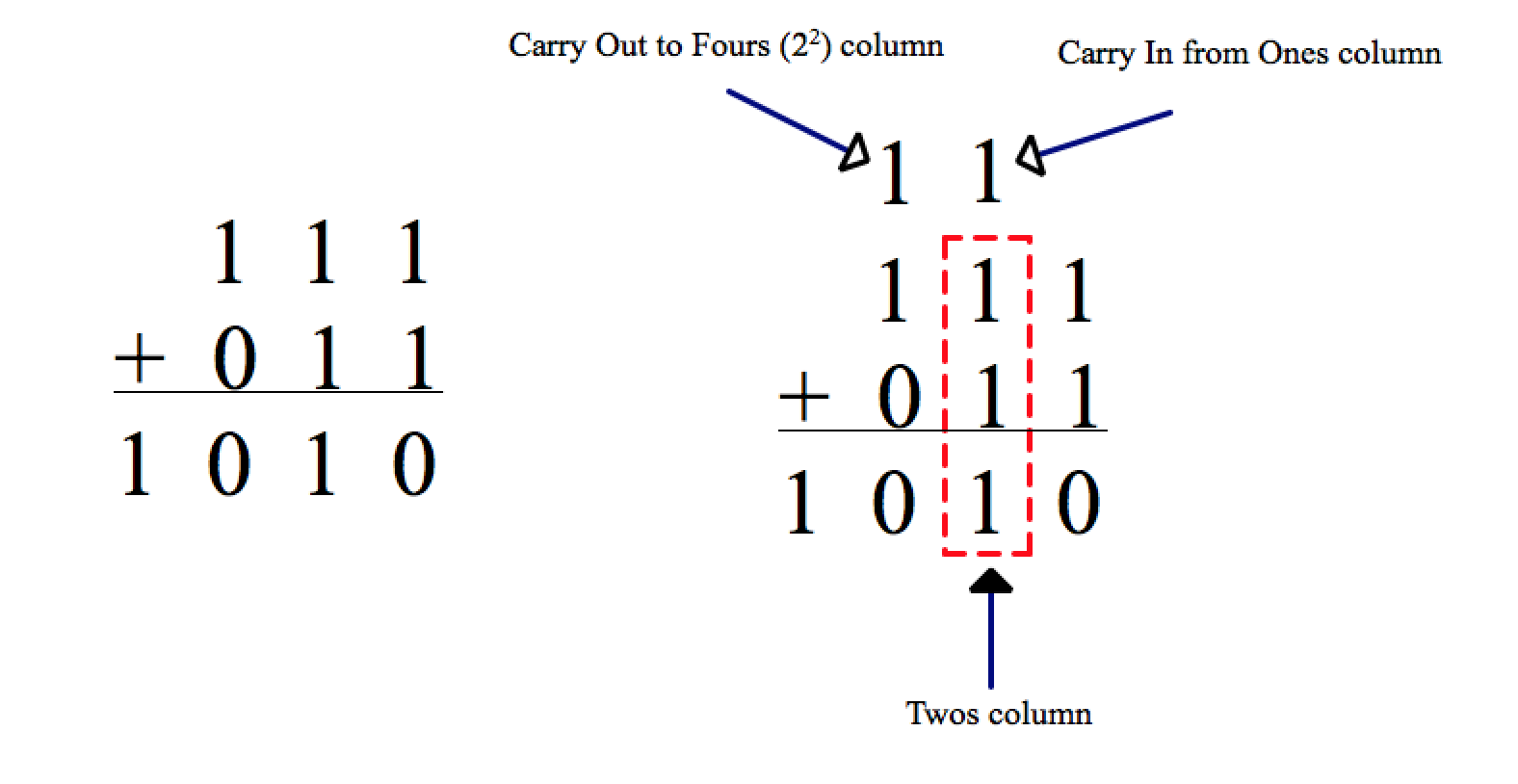
1 + 1 = 10(in English: one plus one equals two)
11 + 1 = 100(in English: three plus one equals four)
It may feel counterintuitive at first 🤯, but there’s nothing fundamentally different about binary compared to decimal, we’re just more used to working in decimal.
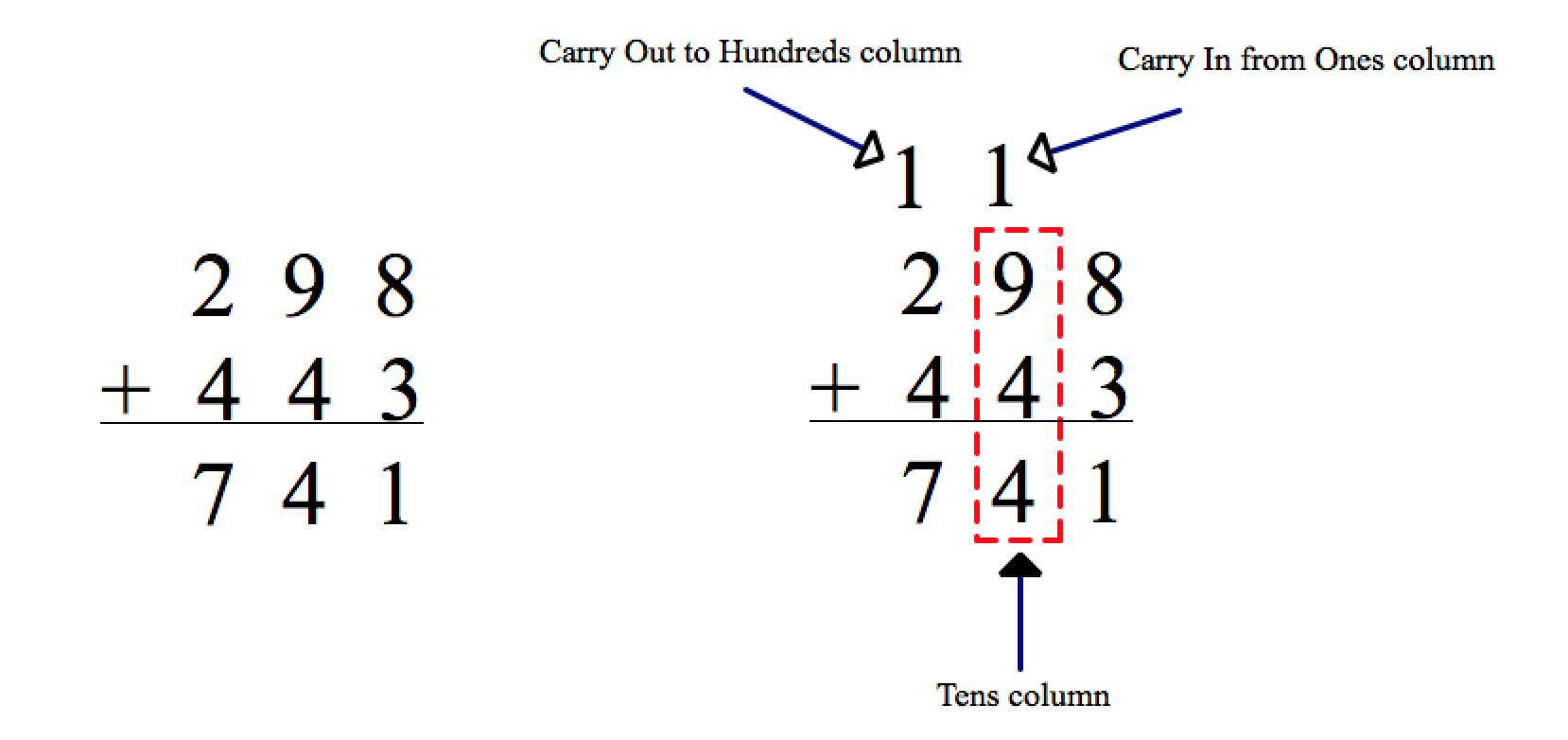
Just like in decimal addition, when a column reaches its maximum digit (9), we carry over a 1 to the next column (the next power of 10). In binary, the idea is the same, but the largest digit is only 1. So whenever we get 1 + 1 in the same column, we carry over to the next place value (the next power of 2).
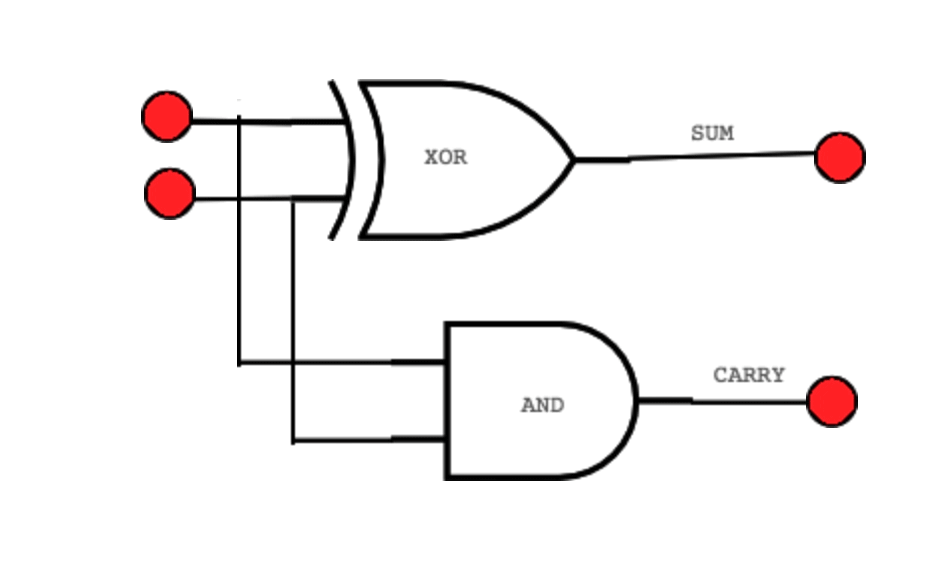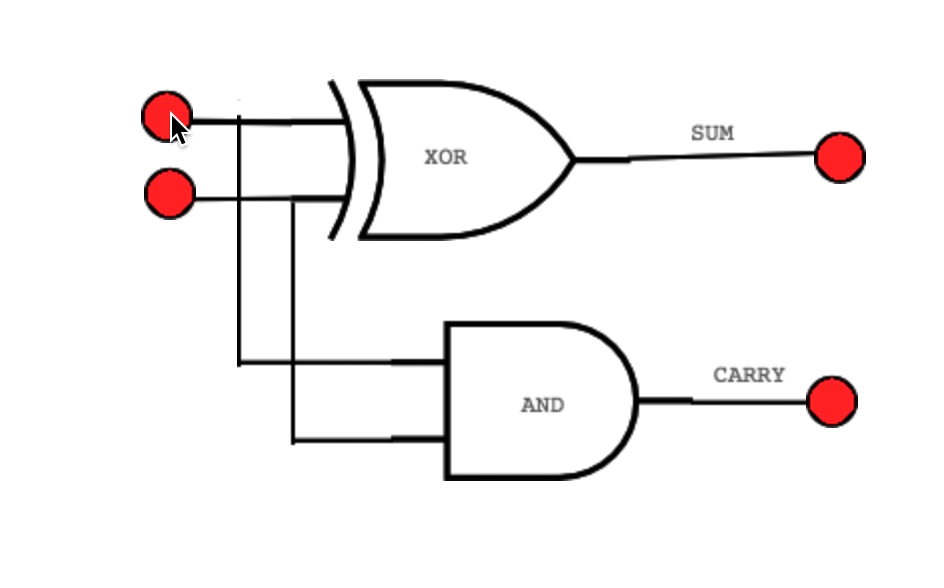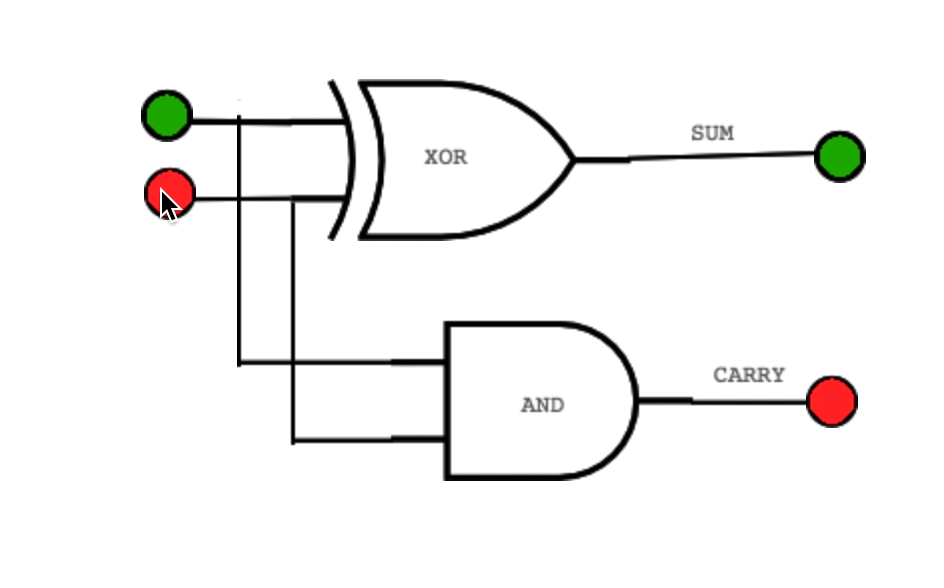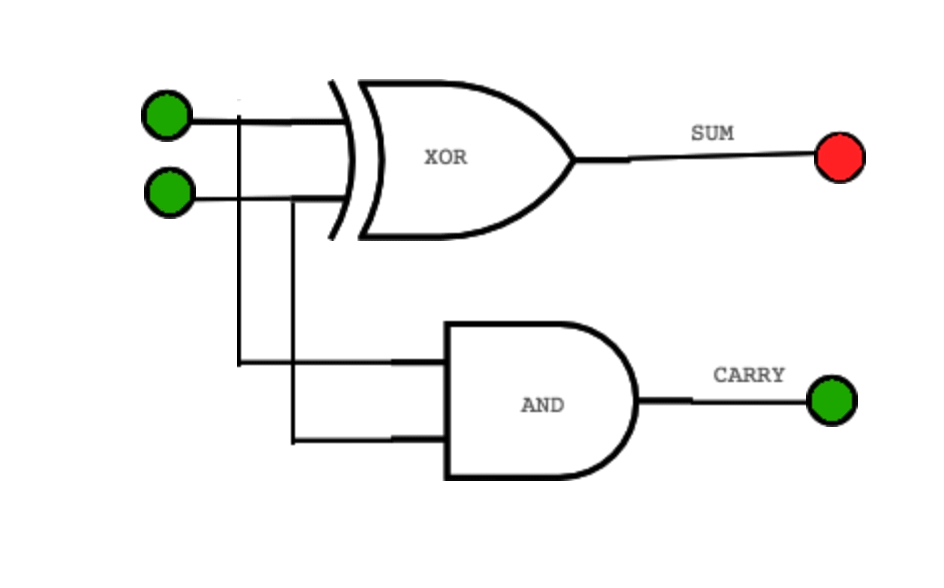
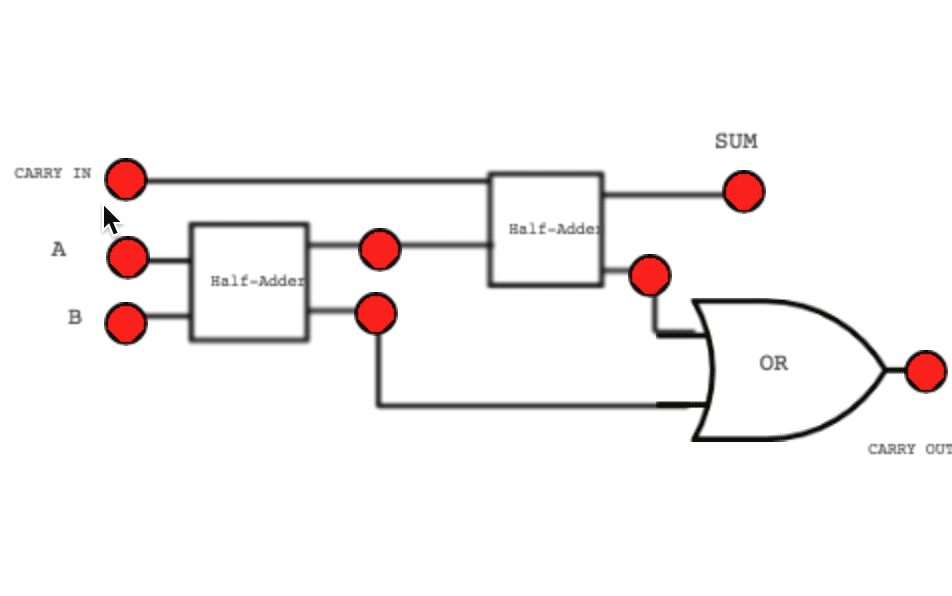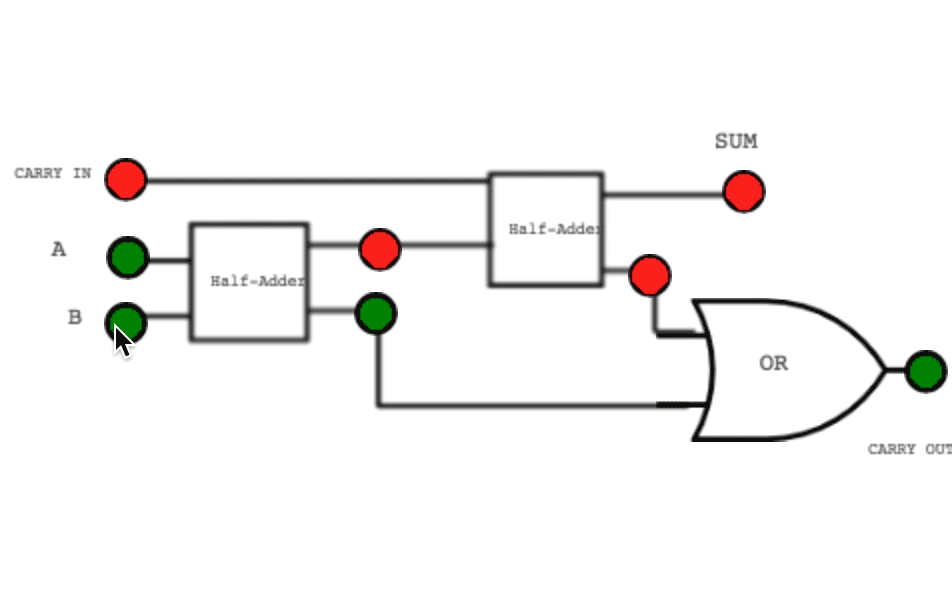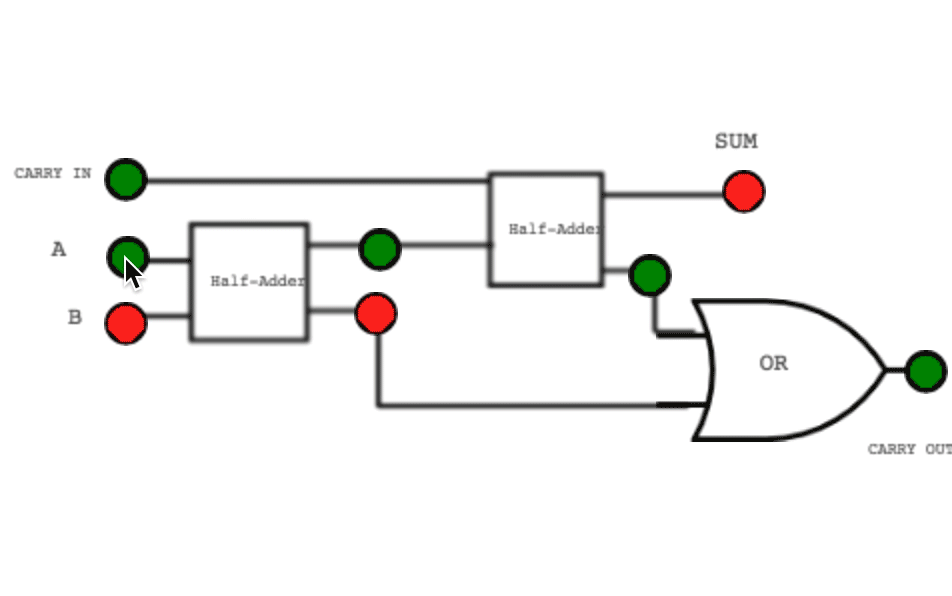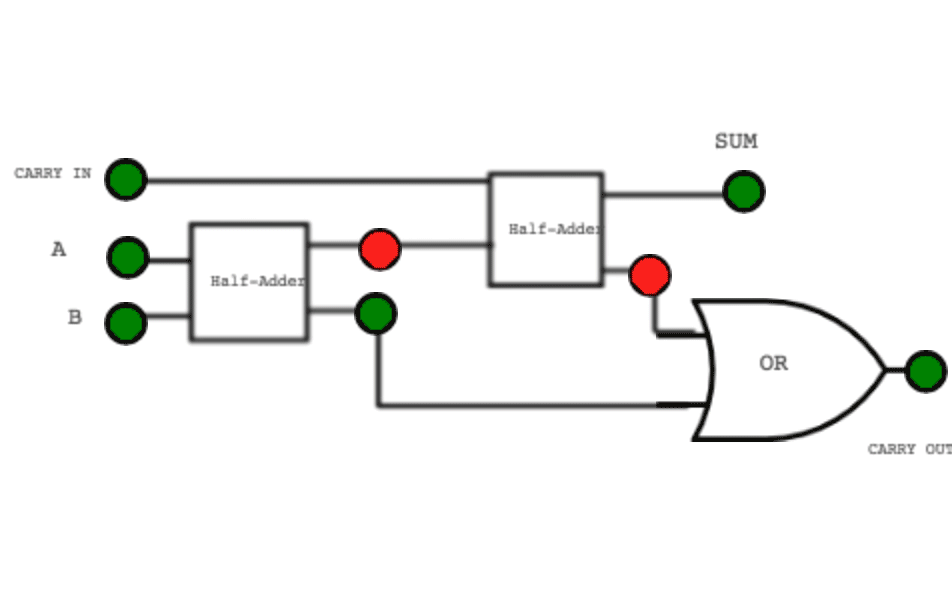
Inside the CPU, special circuits called adder gates handle this process automatically. The sum is the result that stays in the current column, while the carry (C) is the extra 1 that “spills over” into the next column (the next power of 2).
1➕1 Adds two single binary digits.
1➕1➕1: Adds two binary digits and includes the carry from a previous addition.Binary subtractions ➖
When subtracting binary numbers, computer actually convert the left operand to a negative number and performs a simple addition, because this simplifies the hardware of chips. Let’s explore how computers represent negative numbers.
Negative numbers 🌡️
Not all numbers in real life are positive, just think of freezing winter temperatures in Canada 🥶 or when bank accounts slip below zero ☹️💸. Because of this, computers must be able to represent not only positive values but also negative ones. In binary, special methods are used to handle negative numbers so that calculations remain accurate and efficient.
How can be achieve this with a binary system?
The simple answer is to use the first bit of a number to represent the sign and use the remaining bits for the magnitude of the number:
1 for negative ➖
0 for positive ➕
Unsigned versus Signed 🖊️
Up to now, we’ve only looked at positive binary numbers, where all the bits are used to represent the value. For signed numbers, however, one bit is set aside to indicate the sign (positive or negative). This reduces the range of values that can be represented.
For example, with 4 bits we can represent the unsigned numbers: 0 to 15, while with the same number of bits we can represent signed numbers -7 to +7.
With this simple approach however, zero ends up having two representations (positive zero and negative zero), and basic operations are not working as expected, for example: \[ 5_{10} + −5_{10} = 0101_{2} + 1101_{2} = 0010_{2} \not = 0_{10} ❌ \]
\[ 6_{10} + (-2)_{10} = 0110_{2} + 1010_{2} = 0000_{2} \not = 4_{10} ❌ \]
Here are the binary values from -7 to +7:
| Binary | Decimal Value |
|---|---|
| 1 1 1 1 | -7 |
| 1 1 1 0 | -6 |
| 1 1 0 1 | -5 |
| 1 1 0 0 | -4 |
| 1 0 1 1 | -3 |
| 1 0 1 0 | -2 |
| 1 0 0 1 | -1 |
| 1 0 0 0 | -0 ❓ Negative zero?? |
| 0 0 0 0 | 0 ⚠️ Zero appears twice! |
| 0 0 0 1 | 1 |
| 0 0 1 0 | 2 |
| 0 0 1 1 | 3 |
| 0 1 0 0 | 4 |
| 0 1 0 1 | 5 |
| 0 1 1 0 | 6 |
| 0 1 1 1 | 7 |
Two’s complement
Two’s complement is the most common way to represent signed numbers in computers. It’s based on mathematical thoeries and help fix the issues seen above with the “simple approach”.
Example: Representing a negative number using Two’s Complement
✍️ Write the positive version of the number using all the bits available (including one bit for the sign)
- Example: (5)10 = (0000 0101)2
🔄 Invert all the bits (flip 0 → 1 and 1 → 0).
- 0000 0101 → 1111 1010
- This is also called One’s complement.
➕1 Add 1 to the inverted value.
- 1111 1010 + 1 = 1111 1011
✅ Therefore, (-5)10 = (1111 1011)*2
Here are the binary representation of numbers from -7 to +7 in two’s complement:
| Binary | Decimal Value |
|---|---|
| 1 0 0 0 | -8 |
| 1 0 0 1 | -7 |
| 1 0 1 0 | -6 |
| 1 0 1 1 | -5 |
| 1 1 0 0 | -4 |
| 1 1 0 1 | -3 |
| 1 1 1 0 | -2 |
| 1 1 1 1 | -1 |
| 0 0 0 0 | 0 |
| 0 0 0 1 | 1 |
| 0 0 1 0 | 2 |
| 0 0 1 1 | 3 |
| 0 1 0 0 | 4 |
| 0 1 0 1 | 5 |
| 0 1 1 0 | 6 |
| 0 1 1 1 | 7 |
Math operations in Two’s complement
Now let’s observe why Two’s complement fixes the simple operations we had earlier:
🧮 Example 1: \[ 5_{10} + -5_{10} = 0101_{2} + 1011_{2} = 0000_{2} = 0_{10} ✅ \]
🧮 Example 2: \[
6_{10} + -2_{10} = 0110_{2} + 1110_{2} = 0100_{2} = 4_{10} ✅
\] 🔄 The overflow that happens with fixed bits ensures that we “wrap around” back to 0 when adding a positive and its negative counterpart.
💡 Key Advantage:
Using Two’s Complement makes math operations simpler for computers ⚡. Both signed and unsigned numbers can be added using the same adder circuits 🔌.
👉 For example:
- 4 + 2 (unsigned)
- 4 + (-2) (signed)
Both are handled using the same hardware adder gate ➕.